Mi experiencia en un aula para pensar:

María Teresa Pavón Reguera

Tras las JAEM XXI, celebradas en junio de 2024 en Cantabria, con muchas ideas y recursos leí el libro “Building Thinking Classrooms in Mathematics”, de Peter Liljedahl, ahora traducido a español como “Diseñando Aulas para Pensar en Matemáticas”. Tuve la gran suerte de asistir en este congreso al taller que impartía Daniel Ruiz Aguilera, profesor de la Universitat de les Illes Balears, sobre Thinking Classroom.

Durante estos dos últimos cursos he trabajado con mi alumnado actividades de suelo bajo y techo alto, intentando hacerles personas competentes, aprendiendo a pensar para resolver problemas, vamos, lo normal que hacemos todos los docentes. Pero este taller supuso un antes y un después. Si le añadimos la lectura del libro anteriormente citado, no veía el momento de llevarlo a la práctica.

Pero, ¿qué es esto del Thinking Classroom? Podríamos definirlo como un enfoque de enseñanza que prioriza el desarrollo de las habilidades de pensamiento crítico de los estudiantes, la resolución de problemas (curriculares o no) y la colaboración, centrándose en el proceso de aprendizaje más que en la adquisición de conocimiento, que también.

No voy a hacer un spoiler del libro, sino a contaros mi experiencia en este primer trimestre.

Tras conocer al alumnado de 1º ESO, grupos, dificultades, motivaciones e intereses, les hablé de las diferentes metodologías que íbamos a utilizar en la asignatura de matemáticas, de los instrumentos de evaluación (especialmente de las rúbricas) y de las “normas en la clase de matemáticas”, reconocieron que no sabían pensar por ellos mismos. Estaban habituados a realizar actividades y problemas en modo “Control C-Control V”, vamos, de imitación. Por ejemplo, si se les explicaba el concepto de fracciones equivalentes, realizaban una ficha para trabajar este concepto y punto. Si se explicaba el máximo común divisor, se realizaban problemas para aplicar ese concepto y así sucesivamente con todo el temario. Pero desconocían las conexiones entre conceptos o incluso entre “bloques”. En definitiva, no sabían pensar.

Así que, ya os podéis imaginar mi primera pregunta para trabajar el concepto de operaciones con números naturales: usando sólo cuatro cuatros y operaciones combinadas, tratar de obtener los números del cero al diez.

Esta actividad les encantó y pidieron más. Sentí que ellos necesitaban mantener una mentalidad de crecimiento.

El segundo paso fue comprar 9 pizarras de rotulador y colocarlas, con ayuda de los compañeros del Departamento de Tecnología, en el SUM (Salón de Usos Múltiples) y comenzar a trabajar en nuestra “Aula para pensar”.

Una sesión por semana, trabajamos en ella de pie, en grupos de tres visiblemente aleatorios, problemas curriculares o no con unas normas muy bien definidas, y que el alumnado ha aceptado y asimilado en tan solo cuatro sesiones.

Los grupos visiblemente aleatorios se refiere a que, ellos eligen en cada sesión, mediante la extracción de unas cartas numeradas del uno al tres, a sus compañeros de equipo con los que pensar y razonar el problema que se proponga para dicha sesión.

Parece fácil, ¿no? Para nada, los grupos deben cumplir unas normas:

-Sólo un miembro del grupo tiene el rotulador de la pizarra (se lo intercambian cada diez minutos)

-El estudiante que tiene el rotulador no puede escribir en la pizarra sus ideas, sino lo que le indiquen los miembros de su grupo (esto les parece difícil realizarlo)

-No pueden borrar las pizarras hasta que el profesor pase, valore lo que están haciendo y marque con un rotulador de otro color su trabajo.

-El profesor sólo puede responder preguntas para seguir pensando.

-La tarea asignada e instrucciones se dan verbalmente al alumnado de pie, alrededor del profesor y después se distribuyen en sus pizarras.

-Las soluciones se dan al finalizar la clase o incluso en días posteriores para que puedan comprobar si han entendido cómo han trabajado en el grupo.

-Se les pide que justifiquen su pensamiento.

¿Y qué se evalúa y califica? En España trabajamos por competencias. Evaluamos y calificamos los criterios asociados a unas competencias específicas. Disponemos de unos descriptores operativos que nos dan información a cerca de la adquisición de las competencias clave.

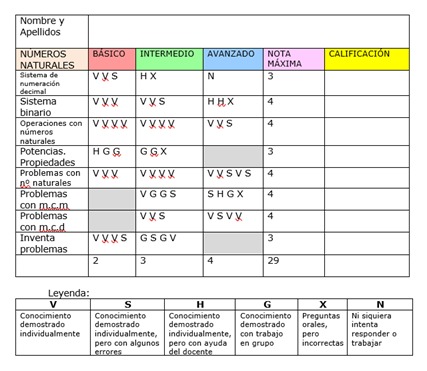
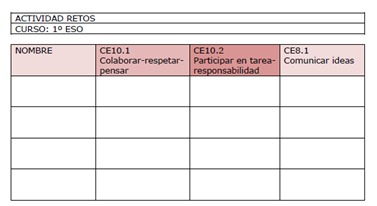
Podemos hacer unas tablas con los indicadores que necesitemos evaluar en cada momento y por cada estudiante, como se muestra en la imagen, o podemos evaluar mediante una rúbrica las competencias específicas que consideremos oportunas.

En mi caso, en este trimestre, decidí evaluar la competencia socioafectiva 10, relacionada con las destrezas sociales, la colaboración, comunicación, planificación, indagación, motivación y confianza, participación, normas de convivencia y responsabilidad individual y grupal. Además de la competencia 8 relacionada con la comunicación individual y colectiva de conceptos, procedimientos y argumentos matemáticos usando la terminología matemática adecuada.

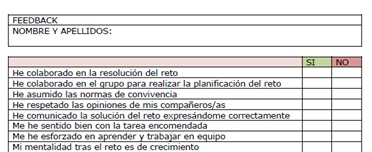
El resultado ha sido muy positivo, favoreciendo el trabajo en equipo y aceptación del grupo-clase, además del desarrollo de habilidades de pensamiento crítico (encuesta anónima realizada al finalizar el trimestre)

Os dejo algunas imágenes de los estudiantes “pensando y razonando” problemas matemáticos en un “Aula para pensar” y os animo a leer el libro y ponerlo en práctica. Vuestro alumnado os lo agradecerá.